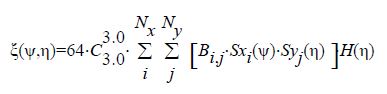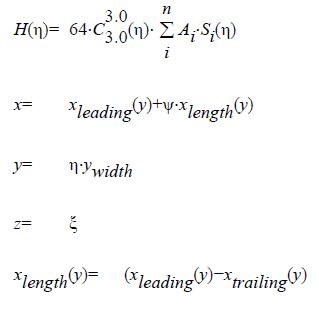The governing equations for the flow are the Reynolds averaged Navier-Stokes equations with the Spalart-Allmaras turbulence model.
The three-dimensional bump is parameterised using the CST method, as an extension of the two-dimensional CST bump using a second Bernstein polynomial. The CST bump patch may not be strictly a rectangle, so the bump length distribution along spanwise is a function of span. The definition of a three-dimensional bump with sweep angle is shown in the following equations:
where
where xleading and xtrailing are the leading edge and trailing edge values of x at a given y, which can be a higher polynomial function depending on the distribution shape. The CST bump equations can provide higher flexibility of a local bump, and generate symmetric or asymmetric bumps in three-dimensional space. The orders of Bernstien polynomials are recommended to be below 4, this allows the CST bump to provide high flexibility with a reasonable number of design variables and produce the most realistic bump shapes.